「標準偏差」はよく使われるデータ分析の指針の一つです。ここでは標準偏差の意味、標準偏差の求め方、なぜ標準偏差を求めるのか? 標準偏差を求めて分かることは何か? などについて、できるだけ分かりやすく図解します。また、標準偏差を簡単に求めることができるExcel関数の使い方も併せて解説します。
標準偏差・SD・σ(シグマ)とは?
標準偏差を学ぼうとすると「SD」という表記や「σ」という記号を目にすると思います。最初にこれらの意味を簡単に説明しておきます。
- SDとは?
- 「SD」は英語の標準偏差「Standard Deviation スタンダード ディビエーション」の略語です。エクセルで標準偏差を求めるための関数名は「SD」ではなく「STDE」ですが、これも「Standard Deviation」の略です。

- σ(シグマ)とは?
- 標準偏差は「σ(シグマ)」という記号で表記されます。シグマはアルファベットの「S」に相当するギリシャ文字です。標準偏差=SDのSを表しています。シグマの大文字「Σ」は合計(SUM)を表す記号で、標準偏差を表すのは小文字の「σ」です。

標準偏差の意味
「偏差」は平均との差分のことで、データと平均値との距離幅を指します。標準偏差とは、統計学において平均値を基準にしたデータのばらつきの目安となる指標の一つです。
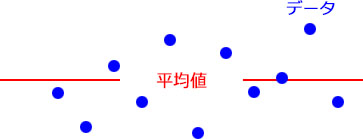
もう少し平たく言うと、標準偏差は平均値からどのくらいの距離にデータが散らばっているかを示す値です。データが平均値からさほど離れずに散らばっていれば「標準偏差」の値は小さく、平均値から距離を持って散らばっていれば「標準偏差」の値は大きくなります。
標準偏差を分かりやすく示す正規分布のグラフ
データの個数を縦軸に、データの数値を横軸にしてグラフを描くと、多くは左右対称の山型になります。このグラフは「正規分布」といい、平均値を中央にしてプラスマイナス「標準偏差の幅」の範囲にデータの約68%が分布します。標準偏差をレクチャする相手に分かりやすく示すために正規分布などのグラフは効果的です。
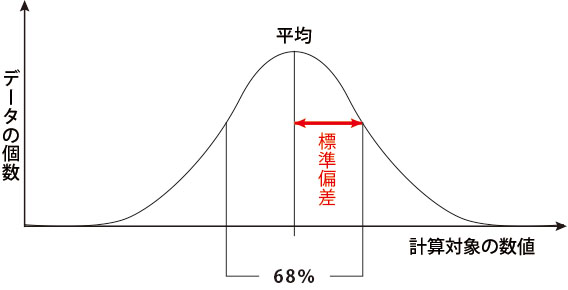
標準偏差の値が小さければ、グラフの山型の幅が狭まり、データの密集度が増します。多くのデータが平均値の近くにあるので、品質管理の検査などでは期待通りの結果ということになります。
標準偏差を求めるのはなぜか?
- 標準偏差を求める理由は第一にデータ分析の指標として優れているという点です。
- データ表の数値から「平均値」を計算して分析の基準にしますが、この値はデータの分布状況を反映していません。
あるクラスのテストの平均点が全国平均を上回ったとしても、そのクラスのほとんどの生徒が全国平均以上の実力を持っているとは限りません。一部の優秀な生徒が底上げしている可能性もあるからです。

クラス全体の実際の優劣を判断するには平均値だけでは無理なので、点数がどのように分布しているかを知るための値が必要になります。その値が「標準偏差」です。
- 標準偏差を求める理由の第二は、イメージしやすさ、説明しやすさです。
- 標準偏差の数値は平均値からデータのばらつきの距離を直感的に把握しやすく、データ分析を説明するのにとても有用なのです。標準偏差と同じく平均値からのばらつきを求める「分散」という統計量がありますが、標準偏差と分散の決定的な違いは「説得力」にあります。
標準偏差を求める前に分散との違いを知る
「標準偏差」と「分散」は混同されやすいので、その違いを説明しておきます。
平均値からのばらつきを計算したいと思ったら、まず「分散」を求めます。「標準偏差」は「分散」に対する平方根の値で、標準偏差と分散は実質同じものです。分散の計算は標準偏差より楽ですが、講義やレポートなどには一般的に標準偏差が使われます。
データの単位は「点数」や「時間」だったり「グラム」だったりします。「分散」はその二乗が単位になります。標準偏差の方は単位がデータと同じなので説明しやすく、数字に説得力を持たせることができます。平均速度が33秒で標準偏差が3.0秒なら、「通常の条件下では30秒から36秒の間での走行が可能です」というような説明ができるわけです。
標準偏差を求めて分かることは?
標準偏差を求めることで分かることはデータの種類によっていろいろです。標準偏差の使用例を挙げてみましょう。
- 品質管理で原材料の配分をデータ化し、抜き取り検査でサンプルデータの標準偏差を求める
→ 標準偏差の値が小さければ配分が均一であり、品質には問題なしと分かる - 学力テストで各自の点数データから標準偏差を求める
→ 標準偏差の値が大きければ学力の個人差が大きく、担任教師が成績下位の生徒の学習意欲を引き出せていないことが分かる - 試作品のアンケートで評価の点数をもとに標準偏差を求める
→ 標準偏差の値が小さければ一般の評価は平均値とほぼ一致していると分かり、平均値が高ければ発売に踏み切る判断材料になる
標本標準偏差と不偏標準偏差の意味や求め方の違い
標準偏差には「標本標準偏差」と「不偏標準偏差」の2種類あります。標準偏差の求め方も「標本標準偏差」と「不偏標準偏差」では違いがあります。
この2つを分けるのは計算するデータの範囲が母集団か標本かです。「母集団」とはデータ全体のことで、「標本」は母集団から無作為抽出したサンプルのことです。
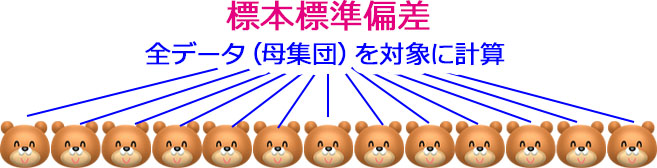
- (標本)標準偏差
- 母集団を対象に計算するのは「標本標準偏差」、或いは単に「標準偏差」です。データの全てを対象に標準偏差を求めます。母集団が限定的なデータ数である場合に使う計算方法で、膨大なデータベースで使うのは現実的ではありません。
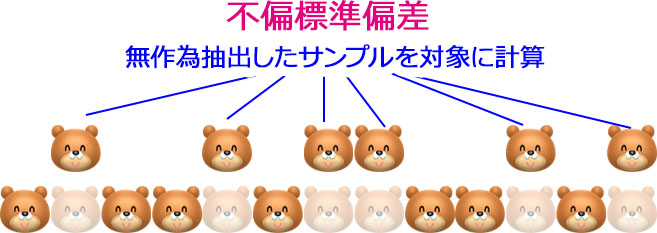
- 不偏標準偏差
- 母集団から無作為抽出した標本を対象に計算するのは「不偏標準偏差」です。サンプリングした標本から標準偏差を求めます。企業がデータ分析をする場合の多くは不偏標準偏差が採用されます。前章の「標準偏差から分かることは?」の例で言えば、品質管理の抜き取り検査で求める標準偏差は「不偏標準偏差」です。
標準偏差の計算式
標準偏差を求めるには、まず「分散」を計算しますが、前述したように「標本標準偏差」と「不偏標準偏差」で違いがあります。
- (標本)標準偏差の分散の計算
- 個々のデータから平均値を引いた値の二乗を全て足し算し、データの個数で割り算します。
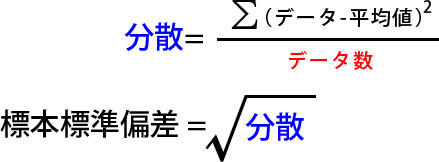
- 不偏標準偏差の分散の計算
- 個々のデータから平均値を引いた値の二乗を全て足し算し、データの個数から1を引いた数で割り算します。
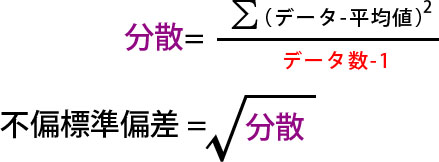
※サンプリングで計算する不偏標準偏差では標本の数が母集団より少ないことから、割る数に「-1」を入れて補正します。 - 電卓で標準偏差を計算
- 「分散」の数値に対する平方根が「標準偏差」ですから、分散値を入力してから√(ルート)を押せば、電卓で標準偏差を計算できます。

標準偏差を求める簡単な計算の例
上のクラス成績の例を使って簡単な標準偏差の計算をしてみましょう。クラスの平均点は「(100+52+48+50)÷4」で「62.5」です。

- それぞれの点数から平均点の62.5を引いて二乗します。
(100-62.5)²=1406.25
(52-62.5)²=110.25
(48-62.5)²=210.25
(50-62.5)²=156.25 - この値の平均値を計算して「分散」を算出します。
(1406.25+110.25+210.25+156.25)÷4=470.75 - 分散値の平方根を計算して「標準偏差」を算出します。
√470.75≒21.69
Excelの関数で標準偏差を求める
Excelには標準偏差を簡単に求めることができる関数が数種類用意されています。
上のクラス成績の例では、母集団の数値を対象に標準偏差を求めるSTDEV.P関数の引数にそれぞれの点数を指定するだけで標準偏差を求めることができます。
計算式はこうなります➔ =STDEV.P(100,52,48,50)
Excelの数式タブで「関数の挿入」か「関数ライブラリ」から「統計」関数の「STDEV.P」の引数ダイアログボックスを開き、数値の欄に標準偏差を求める個々の点数を入力して「OK」を押すだけで標準偏差が計算されます。
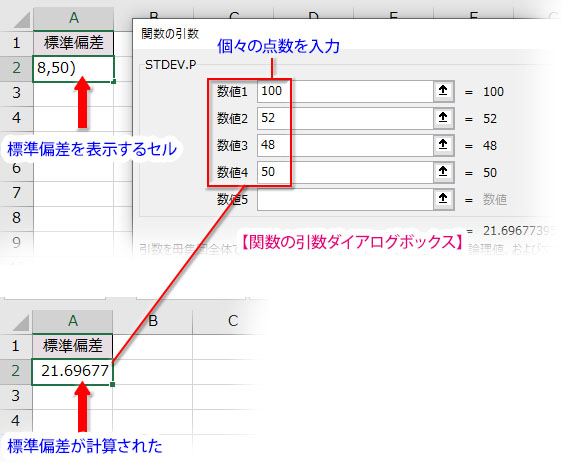
もちろん、実際にはデータ表を作って、その範囲をドラッグで「数値1」に指定することになるでしょう。Excelで関数を使った計算の仕方をもっと詳細に知りたい方は、以下の一覧から各関数の解説ページへアクセスして下さい。
| 関数名 | ライブラリ | 標準偏差の種類 | 仕様 |
|---|---|---|---|
| STDEV.S | 統計 | 不偏標準偏差 | 抜き出した標本の数値を対象に母集団の標準偏差を推定する |
| STDEV.P | 統計 | 標本標準偏差 | 母集団の数値を対象に標準偏差を求める |
| STDEVA | 統計 | 不偏標準偏差 | 抜き出した標本のデータを対象に母集団の標準偏差を推定する |
| STDEVPA | 統計 | 標本標準偏差 | 母集団のデータを対象に標準偏差を求める |
| DSTDEV | データベース | 不偏標準偏差 | 条件を満たすデータから不偏標準偏差を求める |
| DSTDEVP | データベース | 標本標準偏差 | 条件を満たすデータから標本標準偏差を求める |
標準偏差の意味を知り、なぜ求めるかを理解して統計に役立てよう!
標準偏差は平均値からどのくらいの距離にデータのばらつきがあるかを示す値です。なぜ、「標準偏差」を求める必要があるのか、同じように平均からのばらつきを数値化した分散とどう違うのか、標準偏差を求めることで何が分かるのか、このページの解説で理解できたでしょうか?
仕事でデータの統計を取ることは多く、平均値・分散値・標準偏差を計算する場面も多いと思います。標準偏差は電卓でも計算できますが、MicrosoftのOfficeソフトExcel関数を使うと、簡単に求めることができます。この機会にExcelで標準偏差を求める関数にも慣れて、実務での統計作業に役立てましょう。

