「分散」はデータ分析の基本的な統計量です。ここでは分散の意味、分散の求め方、なぜ分散を求める必要があるのかについて、できるだけ分かりやすく図解します。また、簡単に分散を求めることができるExcel関数の使い方も併せて解説します。
分散とは?
統計における「分散」とは「平均値」からのデータの散らばり具合を示す数値です。「分散」は英語ではvariance(ヴァリアンス)。varianceは差異を意味する言葉で、データの個体差が作り出す「ばらつき」を示しています。
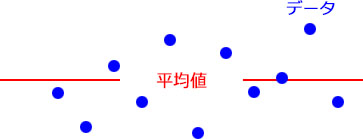
データが平均値からさほど離れずに散らばっていれば「分散」の値は小さく、平均値から距離を持って散らばっていれば「分散」の値は大きくなります。「分散」とは平均値だけでは把握できないデータ分析の指標を数値化したものです。
標本分散と不偏分散とは?
分散には「標本分散」と「不偏分散」の2種類あります。分散の求め方も「標本分散」と「不偏分散」では違いがあります。
この2つを求める違いは計算するデータの範囲が母集団か標本かです。「母集団」とはデータ全体のことで、「標本」は母集団から無作為抽出したサンプルのことです。
- 標本分散
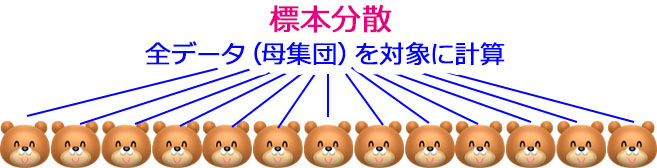
- 母集団を対象に計算するのは「標本分散」、或いは単に「分散」です。データの全てを対象に分散を求めます。母集団が限定的なデータ数である場合に使う計算方法です。
- 不偏分散
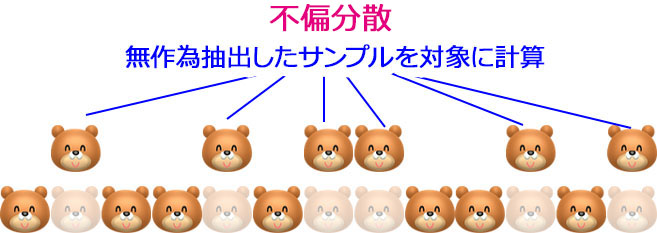
- 母集団から無作為抽出したサンプルを対象に計算するのは「不偏分散」です。サンプリングした標本から分散を求めます。
分散を求める理由と平均との関係
統計で「平均・平均値」は欠かせない基準です。
ですが、単純に全数値の和をデータ個数で割った平均値ではデータ間の優劣を判断するのに必ずしも適正とは言えません。
下図は2つの商品を試食して100点満点で評価したデータ表です。「商品1」と「商品2」の平均値の比較ではどちらも同じ。評価は五分五分と考えていいでしょうか?
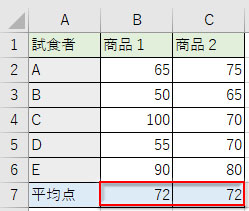
データを仔細に見ると、「商品1」の評価は個人差が大きく「商品2」の評価は平均しているようです。「平均値」の数字ではその辺の状況を示すことができません。そこで、「分散」を求める必要が出てきます。
分散を求める計算式は後述するとして、ここでは取り敢えず「商品1」と「商品2」の分散の数値を表示してみます。
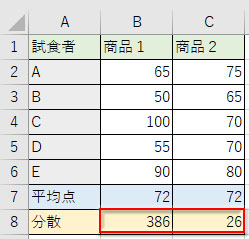
「平均値」は同じなのに「分散」の数値を比較すると「商品1」と「商品2」では大きく違っています。「商品1」は評価が分かれ、バラツキ度が極端です。コアなリピーターは付くかもしれませんが、万人受けする商品ではなさそうです。対して「商品2」はバラツキ度が低く、平均値の評価点は実態に則していると言えるでしょう。
分散を求めるのは「平均」では分からない分析が「分散」を求めることで判断できるようになるというのが理由です。
標準偏差を求める理由と分散との関係
「分散」の数値が平均値では表せない指標を示す有用な分析データであることは分かりました。しかし、「386」「26」という数字は実感が無いというか、ストレートに響いてこない印象です。プレゼンで示しても説得力が今ひとつです。分析データとしてレクチャに使う場合に「標準偏差」が採用されるのは、「分散」に欠けている説得力があるためです。
「標準偏差」は「分散」に対する平方根の値で、標準偏差と分散は実質同じものです。「分散」をルートに入れ、単位もデータと揃えることで、人が扱いやすい数値にしています。
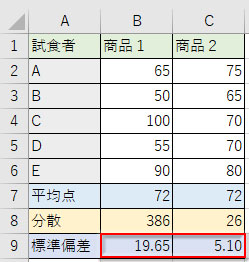
「19.65」「5.1」はそれぞれ平均値からのバラツキの距離を示しています。「商品1は平均値72点から±19.65点の範囲にデータが散らばっており、人によって評価が50点台、90点台に大きく振れるでしょう」と説明できるわけです。
標準偏差については以下の記事で詳しく解説しています

「平均」➔「分散」➔「標準偏差」の流れは、そのまま計算式の流れでもあります。
分散を求める簡単な計算の例
簡単な例題で分散値を求めてみましょう。以下の点数データ4件から分散を計算します。

- 分散を求めるには、まず、データの平均値を計算します。
- 平均値は「データの総和÷データの個数」で求められます。点数をすべて足し算して、データの個数(この例では4)で割り算します。

- 次に、平均値からの偏差(個々のデータと平均値の差)を計算します。
- 偏差は「データの数値-平均値」で求められます。点数から平均値を引き算します。

- 更に、個々のデータの偏差を二乗します。
- なぜ、二乗する必要があるのかというと、「データの数値-平均値」で求められる偏差はプラスの値とマイナスの値が出て、それをただ合計すれば答えは「0」になるだけなので、これを二乗して平均値が最小になるようにします。

- 偏差を二乗した値の平均値を計算して分散を出します。
- 個々のデータの偏差を二乗した値をすべて足し算します。この値をデータの個数で割り算すれば分散が求められます。
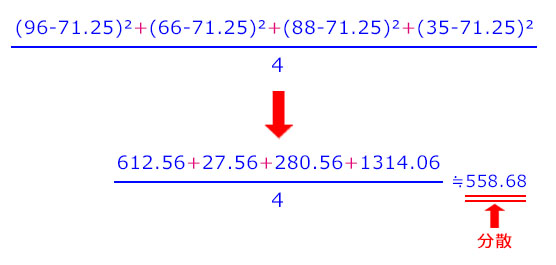
不偏分散の求め方
「不偏分散」では個々のデータから平均値を引いた値の二乗を全て足し算し、データ数-1で割り算して不偏分散を計算します。不偏分散では計算対象のサンプル(標本)数が母集団より少ないことから、割る数に「-1」の補正が入ります。

Excelの関数で分散を求める
Excelには分散を簡単に求めることができる関数が数種類用意されています。
前章の例なら、母集団の数値を対象に分散を求めるVAR.P関数の引数にそれぞれの点数を指定するだけで分散を求めることができます。
計算式はこうなります➔ =VAR.P(96,66,88,35)
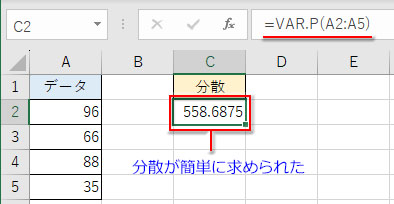
また、Excelの数式タブで「関数の挿入」か「関数ライブラリ」から「統計」関数の「VAR.P」の引数ダイアログボックスを開き、数値の欄に分散を求めるデータ範囲を指定して「OK」を押します。
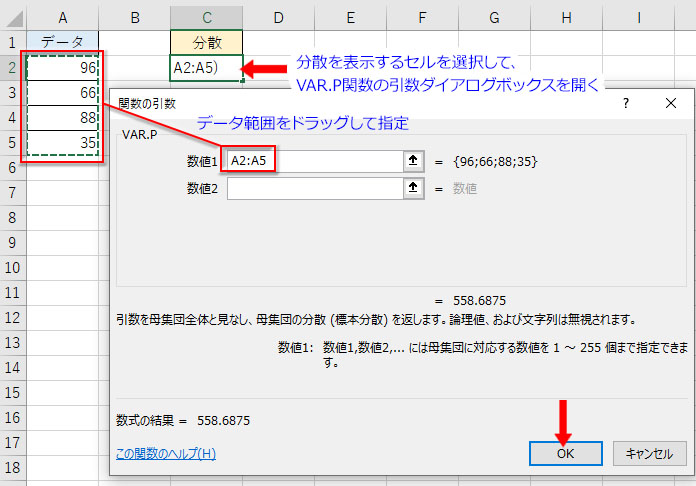
簡単に分散が計算されます。
Excel関数を使った分散の求め方をもっと詳細に知りたい方は、以下の一覧から各関数の解説ページへアクセスして下さい。
| 関数名 | ライブラリ | 分散の種類 | 仕様 |
|---|---|---|---|
| VAR.S | 統計 | 不偏分散 | 抜き出した標本の数値を対象に母集団の分散を推定する |
| VAR.P | 統計 | 分散 | 母集団の数値を対象に分散を求める |
| VARA | 統計 | 不偏分散 | 抜き出した標本のデータを対象に母集団の分散を推定する |
| VARPA | 統計 | 分散 | 母集団のデータを対象に分散を求める |
| DVAR | データベース | 不偏分散 | 条件を満たすデータから不偏分散を求める |
| DVARP | データベース | 分散 | 条件を満たすデータから分散を求める |
分散の意味を知り、なぜ求めるかを理解して統計に役立てよう!
分散は平均値からどのくらいの距離にデータのばらつきがあるかを示す値です。なぜ、平均値からのデータのばらつきを数値化した「分散」を求める必要があるのか、このページの解説で理解できたでしょうか?
「平均」から「分散」、さらに「分散」から「標準偏差」を求める流れを分かりやすくまとめたつもりです。
分散は電卓でも計算できますが、MicrosoftのOfficeソフトExcel関数を使うと、簡単に求めることができます。この機会にExcelで分散を求める関数にも慣れて、実務での統計作業に役立てましょう。

