Excel(エクセル)で中央値を求めるMEDIAN関数の使い方
使用関数:MEDIAN
中央値とは?
数値を大きさの順に並べた時に、ちょうど真ん中に位置する値を中央値と言います。「10・20・30・40・50」のように並んだ数値があれば、その中央値は「30」ということですね。中央値がどのようなものに使われるかというと、最も平均的な値を知りたいが個体差が大きくなるデータ――例えば、年代や職種別の年収やボーナス・貯蓄などの統計でよく目にします。
英語ではメディアン(MEDIAN)。ここで紹介するMEDIANは、中央値を求めるExcelの統計関数の一つです。
MEDIAN関数の書式
「数式」タブ「関数ライブラリ」→「その他の関数」→「統計」→ MEDIANをクリックします。
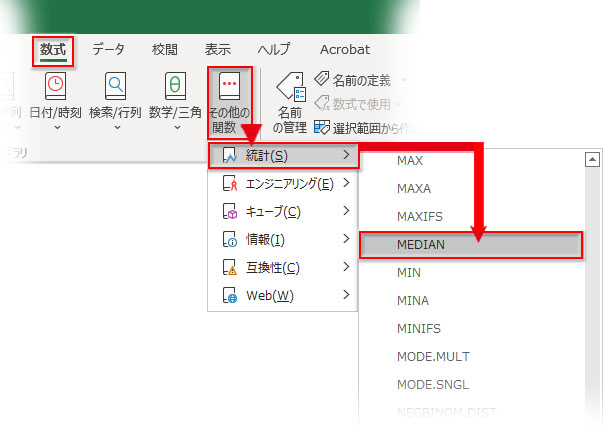
MEDIAN関数の引数は「数値1」が必須で、「数値2」以下は任意です。
書式の構成はこうなります。
![]()
MEDIAN関数で中央値を求める
成人男性の身長データをサンプリングした表でMEDIAN関数を実行してみましょう。
MEDIAN関数の引数ダイアログで「数値1」に身長データの範囲をドラッグで指定します。
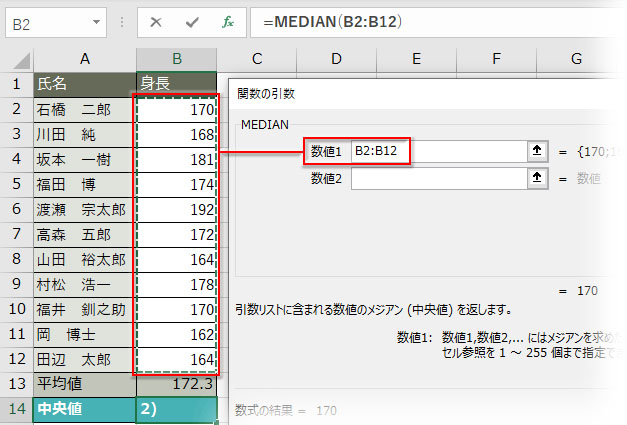
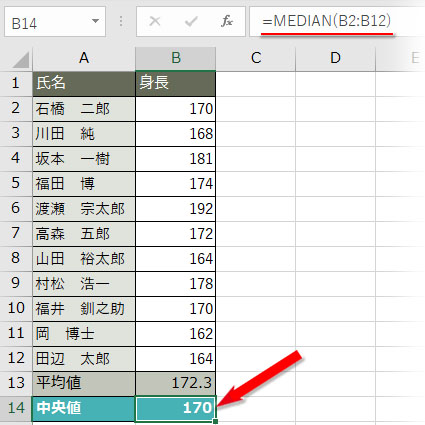
中央値が求められました。
身長データを昇順で並べ替えてみると分かりやすいと思いますが、上下とも6番目の位置にくる値が中央値として取得されています。
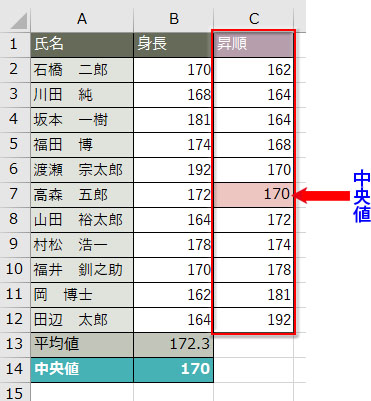
この例のようにデータ数が奇数であれば中央値は一つなので迷うことはありませんが、偶数の場合はどうでしょう?
データ数が偶数の場合の中央値の求め方
中央値を求めるデータが偶数であれば、中央値に相当する値は2つになります。
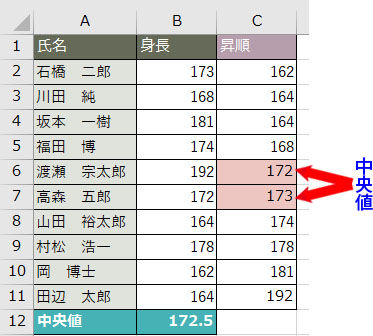
この場合MEDIAN関数は2つの中央値の平均値を返します。上記例なら172cmと173cmの平均値172.5cmが中央値になります。
中央値と平均値の使い分けのポイント
中央値は平均値、最頻値(さいひんち)とセットで説明されることの多い統計用語です。3つともデータ群における中心的な位置を示す値で、「代表値」または「要約統計量」と呼ばれます。
最も一般的な代表値は平均ですが、データの総和をデータ個数で割り算して求める平均値は異常値や外れ値の影響を受けやすい特徴があります。飛び抜けて大きな(または小さな)数値が一つ混じると平均値は変動し、正確な代表値からは遠くなります。対して、中央値・最頻値は極端な大きさのデータが入り込んでも、その影響をほとんど受けません。
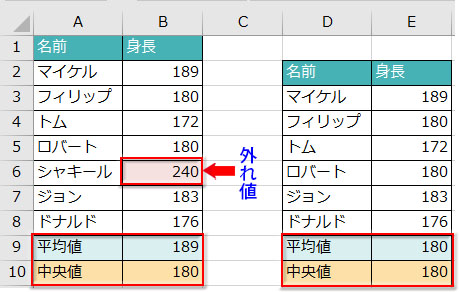
下図の例では男子高校生の身長データの中に一つNBAにスカウトされた男子の身長データが混ざっています。このデータが外れ値で平均値を押し上げていますが、中央値の方は変わりません。外れ値を除いて集計し直した表が右横にありますが、ここでは平均値・中央値とも同じ結果が返っています。
外れ値や異常値のない正規分布(左右対称の釣鐘型を描くような分布)では中央値と平均値が同じか極めて近い値になります。
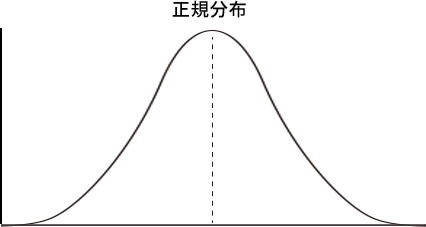
このような安定的な分布のデータでは平均値・中央値のどちらでも同じですが、Excelの関数で代表値を求めるなら、オートSUMから実行できる平均(Average)の方が操作が簡単です。
分布に偏りのあるデータでは中央値の方が実態を正確に反映した数値になります。異常値や外れ値が入り込みやすいデータの代表値には中央値を採用するのが妥当でしょう。
度数分布表やヒストグラムから中央値を求める
「度数分布表」は階級というデータの区間を分類して、その区間のデータ数を表にしたものです。この「度数分布表」から作成するグラフが「ヒストグラム」で、データの代表値を直感的、視覚的に読み取ることができます。
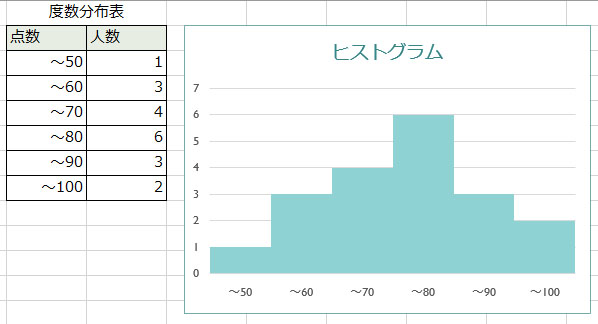
度数分布表とヒストグラムから中央値を求めることもできます。
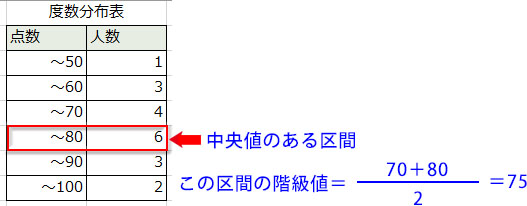
中央値があるのはデータ数の真ん中。データ数が19なら10番目の位置です。度数分布表の「度数(上図では人数)」を上から足していくと10番目の中央値は「階級(上図では点数)」の「~80」の区間にあることが分かります。「~80」は「70より大きく80以下」という意味で、この幅の「階級値」がデータの中央値に当たります。階級値の求め方は、一つ前の区間の上限値(この例では70)と当該区間の上限値(この例では80)を足して2で割ります。この例では75が中央値になります。
度数分布表とヒストグラムの作り方を分かりやすくまとめています。

- MEDIAN(メディアン)は中央値を求める関数です
- 中央値とは数値を大きさの順に並べた時に、ちょうど真ん中に位置する値です
- データ数が偶数の場合、中央値は真ん中に位置する2つの数値の平均になります
- 平均値・中央値・最頻値は代表値と呼ばれ、データ群の中心的な位置を示す値です
- 平均値は異常値や外れ値の影響で上下に大振れしますが、中央値は安定した値を返します
- 度数分布表やヒストグラムから中央値を求めるには、中央値が属する区間の階級値を計算します

